In the previous article, I explored the idea of starting from scratch to develop a framework for understanding practical chess, anchoring our approach in the most concrete and reliable element available – the actual experience of playing chess.
That being said, let’s carry on.
Let’s begin by stating our first axiom, which I would imagine is quite uncontroversial.
Axiom 1: Improving at chess involves playing better moves, on average, over a large number of positions.
This axiom is formulated to avoid oversimplification, which would be the case if it simply stated, ‘Improving at chess involves playing better moves’.
It’s not just about making better moves in a vacuum but about consistently making better moves across various positions encountered in games. Thus, the focus isn’t on isolated instances but on the average improvement over a large number of positions.
—– Quick Note on Formatting ——
You might wonder why I use a structured format of axioms and conclusions throughout these articles. While I acknowledge that this approach may seem pedantic at times, it’s important to understand that the practice of clearly outlining one’s assumptions and the conclusions derived from them is fundamental to all argumentation. Typically, such assumptions are implied rather than explicitly stated. My choice of this format aims to enhance clarity and thoroughness.
Moreover, my experience in presenting arguments online has shown that people often skim content, missing key details, and then, leveraging the anonymity of the internet, leave dismissive or rude comments. Often, as has already happened, people tell me I’m spewing nonsense – but isn’t that a universal experience for anyone presenting arguments online (Right, everyone?….). Therefore, this structured format also simplifies the critique process, allowing critics to clearly identify and challenge specific assumptions or conceptual leaps that they disagree with.
Known and Unknown Positions
Before advancing beyond our rather banal first axiom, let’s define a few concepts that, while seemingly obvious, will be useful for our purposes: ‘Known’ and ‘Unknown’ Positions.
Known positions are those where a player already knows the move they intend to make, without needing further deliberation, typically because they have encountered that exact position before.
For instance, consider the game’s starting position – a known position for almost all chess players. In such cases, players often have a preferred opening move, like 1.e4 or 1.Nf3, though they may still consider other viable options (for instance, maybe they play both 1.e4 and 1.Nf3).
Despite the potential for minor deliberation between these options, the position remains ‘known’ because the player is familiar with the moves and their implications. In the terms of modern chess, known positions generally include any position included in one’s opening preparation.
Conversely, ‘Unknown Positions’ are those in which a player has not pre-decided on a move. These positions require active analysis and decision-making at the moment. Clearly, unknown positions comprise the majority of positions you will encounter as a chess player. It’s important to note that an Unknown Position isn’t necessarily one that the player has never seen; rather, it may be a position they have seen but cannot recall their preferred move (for example, they have forgotten their opening preparation in a given position).
Given this, we can now state our second axiom:
Axiom 2: Chess positions are either known or unknown.
I think that this is fairly reasonable. Every chess position falls into one of two categories: it is either a known position – one that the player has previously encountered and can respond to without further analysis – or an unknown position, which requires analysis before the player can make an informed decision.
In the terminology of modern chess culture, known positions largely encompass opening preparation and theoretical endgames, while unknown positions cover virtually everything else.
Furthermore, I think it’s clear that the majority of chess skill depends on a player’s ability to handle unknown positions. Memorizing positions can only take you so far given the highly variable nature of chess. Chess is not as straightforward as games with limited possibilities like noughts and crosses, where outcomes can be more readily anticipated.
Moreover, even if your opponent has memorized more positions, you can still rely on your skills in unknown positions to find good moves.
Again in the language of modern chess culture – knowing endless amounts of opening theory is not so important if you cannot play well ‘on your own’. It is well understood that a grandmaster is still very likely to beat a club player even if the club player has memorized more theory.
This understanding leads us to our third axiom:
Axiom 3: Almost all of chess improvement is equivalent to playing better moves, on average, over a large number of unknown positions.
We use the term ‘almost’ because a smaller aspect of chess improvement involves expanding the repertoire of known positions through memorization. For example, memorizing opening theory or theoretical endgames. While this topic is important, its relative minor significance means we will focus primarily on how players navigate unknown positions.
However, even after these distinctions are made, we still have a somewhat intimidating task ahead of us – how are we to make better moves in unknown positions?
This query can effectively be distilled into another, more actionable question: ‘How can I make better decisions while analyzing a chess position?’ Essentially, making better moves in unknown positions is tantamount to enhancing the quality of decisions regarding which moves to play on the board. This allows us to transform our last statement into a more insightful form:
Axiom 4: Almost all of chess improvement is equivalent to making better decisions, on average, over a large number of unknown positions.
I actually originally had the first axiom as “Axiom 1: Improving at chess is equivalent to improving one’s decision making, on average, over a large number of positions.”
However, I realized that this wasn’t exactly correct. This is because in known positions, by definition, one is already familiar with the position and knows what they will play. Hence, there isn’t much decision making to be had.
To put it in simpler terms, chess improvement doesn’t just involve making decisions in unknown positions, but also partially involves memorizing what to play in specific known positions.
Therefore, we have first split chess positions into the categories of known and unknown positions to be more precise and accurate. We then assert that chess skill involves not only decision-making in unknown scenarios but also the extent of one’s knowledge of known positions. However, the emphasis remains more heavily on decision-making in unknown positions, as reflected in Axiom 3.
— Side Note —
Defining ‘known position ability’ requires nuance. It’s not merely about the sheer volume of known positions but also their relevance and impact. For instance, extensive knowledge of the Caro-Kann opening theory holds little value if you neither play nor encounter it in games. Conversely, memorizing in-depth theory in an opening like the Najdorf could be significantly more beneficial than in less dynamic openings like the French Exchange. While this topic merits deeper exploration, our current focus will primarily be on unknown positions.
———
Returning to our fourth axiom, it posits that chess improvement largely hinges on making better decisions. Some might think that this concept, like the idea of ‘playing better moves’, sounds equally vague and general, rendering our discussion thus far unproductive.
However, I disagree, since this rephrasing allows us to see what our next step should be: understanding how we make decisions.
To truly understand how to improve at chess, we must first grasp how decisions are made at the chessboard. It’s only after we comprehend the decision-making process itself that we can deconstruct this broad concept into its constituent elements. For example, we might conceptualize the decision-making process as involving elements A, B, and C. By identifying these elements, we can pinpoint where our decision-making falters. Are mistakes arising from a deficiency in element A, B, or C, or perhaps from a combination of several? Recognizing which aspects of the process are deficient provides us the necessary insights to determine precisely how to improve.
Given all of this, our next general goal will be to deconstruct the decision making process into its constituent elements.
The Decision Making Process
Given that getting better at chess ultimately comes down to making better decisions, it’s remarkable how foreign this consideration is to most within modern chess culture. When someone suggests some way to get better at chess, and I question how that helps me make better decisions, people are often taken aback, as if it’s a strange question to ask. It’s as if the connection between improvement and decision-making in chess is an odd concept to consider.
However, of course that’s fundamentally all playing chess is – making decisions.
Now that we appreciate how important understanding the decision-making process is, let’s begin analyzing how these decisions are actually made. This analysis will help us break down the decision-making process into its constituent elements.
To do so, let’s finally get to some chess.
Have a think about this position, what would you play? I’d encourage you to note down your stream of consciousness while thinking about this position, if possible.
Here’s a transcription of how I thought about this position:
Position looks pretty good. Immediately Nf6-e4 looks good. I should stop, considering some other moves first. Bh4 is possible since g3 runs into d5 knight moves. f6 is also possible kicking the knight, but that takes away f6 from my knight. Overall I feel like I should move my d5 knight since it doesn’t feel natural there. Maybe I can bring my queen to d5 too later. Re8 is possible but I can’t see it doing anything anytime soon. Okay so back to Bh4, perhaps just Re2 and I’m not sure that’s an improvement. Maybe also Nc3 sacrifice ideas, but just Bxc3 bxc3 Qxc3 and I don’t see much there. Thankfully I don’t have to consider Na5 ideas since my queen covers that. Bf6 is possible, but no I don’t want to take e5. Nb6 is possible but no that doesn’t look right. Overall I think I like Nf6. It seems to threaten Ne4 too. I need to consider d5 after Nf6, but that doesn’t look good, just Ne4 if I’m trying for the maximum, but at the very least Qxd5. Okay so now Nf6 Re2…
Of course, I could go further here. If I had a lot of time on my clock, I’d probably start looking at more options for white after Nf6, like Re2 as I noted. If I had less time on my clock maybe I’d just play Nf6 at this stage. But all of that is besides the point, since I think we have enough initial data to start thinking about how this decision-making process is working.
Reflect on your own decision making process – did it resemble mine? Not in the sense of the exact moves I was considering, but with respect to the general process? Perhaps your thought process was somewhat similar, but maybe it also incorporated aspects from modern chess. For example, maybe you were thinking something along the lines of:
Black has the bishop pair. Also, white has a bad bishop. Furthermore, white’s light squares – especially in the centre of the board – are extremely weak. White’s knights are also somewhat superfluous. It’s for these reasons that black is better here (Side note: We will come back to such statements – and the role they play in the decision making process – when we consider justification in chess in part 4 of this series). The knight on d5 looks impressive, but really it doesn’t do anything. It also blocks our bishop. We can play Nc7 to open up the bishop, and also prepare Ne6 putting pressure on d4. That looks good – I’ll play Nc7.
Or perhaps you thought:
White’s knight on e5 is really strong, I should play f6 to force it away, and then I’ll permanently cover the e5 square so that white can never use it again. Yes, I’ll play f6.
Or maybe you thought:
I can see that after Nxf4, if white plays Qxf4 then I have Bg5 getting the rook which is good. Instead if white plays Rxf4 I still have Bg5 and that also gets a rook which is good for me. Okay let’s go with Nxf4.
Seeing and Evaluating
Earlier I asked whether your thoughts resemble mine with respect to the general process (and not the specific moves themselves). You may be asking, what general process am I referring to? What general process is common across all of these examples? After all, they all look quite different.
I contend that there are two fundamental processes occurring within all of these examples. Furthermore, I believe these two processes are present when making almost all decisions in chess.
These are Seeing and Evaluating (for now we will call this evaluating, since I think it’s a familiar concept. However, later I will refine the concept to something that I think is more appropriate).
I think these concepts are fairly easy to grasp. Seeing is simply finding new moves that you hadn’t previously considered (for either you or your opponent), and evaluating is determining if you like or dislike (or are indifferent to) the resulting positions. First you look around, and consider some moves. Maybe some moves stick out to you as appealing straight away (such as Nf6 did to me, or as Nxf4 did to the person in the last example).
Maybe you’re not too sure (not confident in your evaluations) after looking at a first set of moves, and so you start looking for new ideas. Then you consider some responses from your opponent, and you evaluate those resulting positions and so on. You can think about this process in a very ‘computerish’ way using a tree of variations. For example, the following tree may roughly represent where I was at after my analysis of the position.
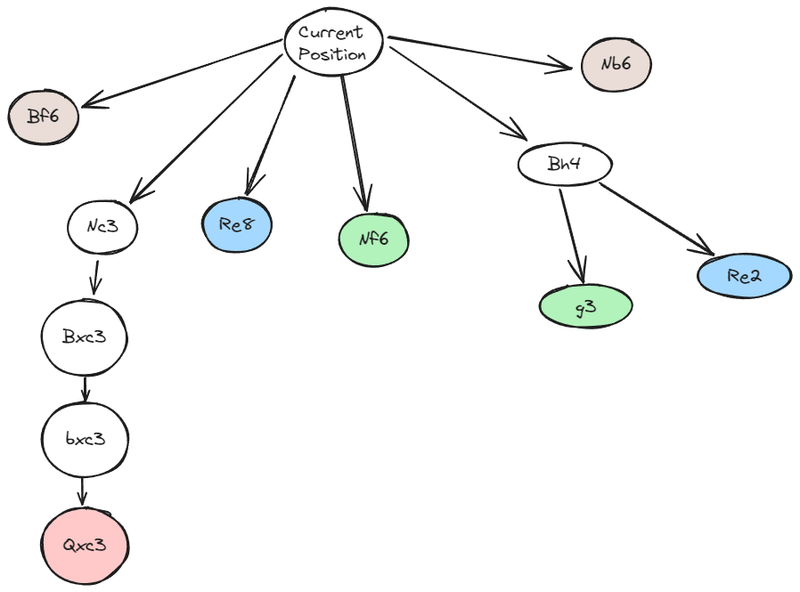
In this diagram I’ve chosen to use colors to represent how I felt about the resulting positions (green being good for me relative to the current position, blue being not too different, gray meaning I’m not such a fan, and red meaning not good). Using this representation, we can now better understand these two processes – seeing and evaluating. Seeing is equivalent to adding new nodes to the tree, and evaluating is equivalent to assigning colors to the nodes. Of course, strictly speaking the intermediary nodes should also be colored. For example, Bh4 would be blue, since the worst outcome for us – Re2 – would be blue. Then, Nc3 would be red (assuming we didn’t have any better options than bxc3 after Bxc3). But I digress. The aim here isn’t to rigorously define how these charts should be constructed, rather it is merely to offer a new way to think about these two fundamental processes – seeing and evaluating. Seeing = adding new nodes, evaluating = assigning colors.
I’ll note here that this isn’t exactly right. This line of thinking makes it seems as though these processes are operating independently, which I don’t believe to be the case. Rather, I think this ‘evaluating’ ability has a large impact on what we see. This is one of the main reasons why I will rename this ability of ‘evaluating’ later on, as that word gives the wrong impression. For the moment, though, we’ll continue with the understanding presented above, similar to how the plum pudding model was a placeholder before the quantum model provided a more accurate representation of the atom.
This brings us to the introduction of Axiom 5:
Axiom 5: In all unknown chess positions, the decision-making process consists solely of two fundamental processes – seeing and evaluating.
I limit this axiom to unknown positions because, by definition, in known positions the player has predetermined their move without needing further deliberation. In contrast, unknown positions, where deeper analysis is required, are governed by these two distinct but interconnected processes, seeing and evaluating.
Note that I claim that these are the two fundamental processes involved in decision making. In other words, there may be other processes going on too, however, they will all be in service of one of these two processes.
For example, perhaps you apply the principles that you learned from book X to help you evaluate a position (which I think is impossible, but more on that in the next later article in this series). In this case, those principles are merely a tool to assist with the more fundamental process of evaluating. Maybe you do a voodoo dance, spin around and clap three times and then you’re able to see moves that you didn’t see before. Again, this tool is serving the deeper process of seeing.
I am of course only a single individual, and hence I only know my own thoughts when playing chess – I cannot peep inside the minds of others while they play. However, after talking to and analyzing with thousands of chess players, as well as listening to many chess commentators, live streamers and in general being involved in the chess world for most of my life, I am convinced that this process is universal. I am convinced that every chess player, whether it be a beginner or a world champion, has a general thought process similar to mine and to the examples previously given. These thought processes might differ in their level of organization of thought, or in the particular words used while thinking, or in the speed of execution; however, the fundamental process is the same – you are either adding nodes, or coloring nodes.
Hopefully you agree with this. Maybe you even think that this is obvious. Perhaps you think something along the lines of:
Jack, duh! Everybody already knows that, and you’re just making things sound more complex than necessary. ‘Seeing’ is just like being good at tactics and stuff, as well as knowing the typical ideas in those types of positions and making sure to consider all of your candidate moves. Evaluating comes from having a deep understanding of chess and knowing what the typical ideas are for that kind of position….
and so on.
If that’s you, then great! I’m glad you agree. However, please be patient – sometimes obvious observations can lead to more fruitful conclusions with just a few more steps.
Some Interesting Consequences
Accepting our initial axioms already leads to some interesting conclusions. For example, most of the time when you make a mistake in chess, it’s either because of a lack of vision, or because of incorrect evaluation (the reason I say ‘most of the time’ is because there is some nuance here. For example, if you miss a move when in time pressure, is your error due to your lack of vision, or with another aspect of your play that caused you to get into time pressure? We will discuss related concepts of focus, efficiency and time management when we discuss calculation in a later article).
Flawed Vision
You may be familiar with the experience of playing a game, and then when you analyze the game with an engine afterwards you see a big spike in the evaluation, suggesting that there was an important moment where you didn’t capitalize on your opponent’s mistake. When you go to see what the correct move was, it instantly strikes you as a great move. You do not need any convincing – if you had considered that move during the game, you no doubt would have played it. In this case, your vision let you down.
Flawed Evaluation
On the other hand, sometimes there are games where you are not too sure where you went wrong, even after briefly analyzing it. When analyzing the game with a computer, you did indeed consider the moves that the engine recommends; however, when considering the resultant positions, you didn’t get the sense that they were promising. In other words, you didn’t miss any moves, rather, your evaluation was off.
I’ll also quickly note here that the process of deconstructing chess ability into discrete sub-skills isn’t unique. In fact, there are countless ways of doing so. For instance, one might argue that chess proficiency hinges on either one’s skill in blitz or non-blitz games. Alternatively, you could say that it depends on your ability in positions resulting from the Najdorf opening and positions not resulting from the Najdorf opening. Both of these statements are true. Furthermore, you could say that every time you make a mistake in chess, it’s either a ‘non-Najdorf mistake’ or a ‘Najdorf mistake’.
However, while these distinctions are valid, I don’t think they will be very helpful when trying to answer our question of improvement. On the other hand, I propose that segmenting chess ability into seeing and evaluating is not only accurate but also useful for conceptualizing practical chess. This discussion just now is very much related to the idea of pragmatism in chess covered in the previous article in this series – we are free to adopt whatever conceptual model we like, as long as it helps us achieve our goals.
Referring back to our initial axioms, we now have:
- Axiom 4: Almost all of chess improvement is equivalent to making better decisions, on average, over a large number of unknown positions.
- Axiom 5: In all unknown chess positions, the decision making process consists of two and only two fundamental processes – seeing and evaluating.
- Conclusion 1: Almost all of chess improvement is either improving your ability to see – your chess vision – or your ability to evaluate.
We could continue to deduce some other conclusions from our available axioms, however, they wouldn’t be of much consequence at the moment and so we will refrain from doing so for now.
Let’s roughly review what we have covered so far: Improving at chess translates to consistently playing better moves, on average, across a large number of positions. Chess positions are categorized as either known or unknown. The majority of chess proficiency relies on making better moves in unknown positions, which in turn, is dependent on making better decisions in these scenarios. Given that the decision-making in unknown positions fundamentally involves seeing and evaluating, it follows that most of chess improvement hinges on refining these two abilities.
This diagram summarizes what we have so far:
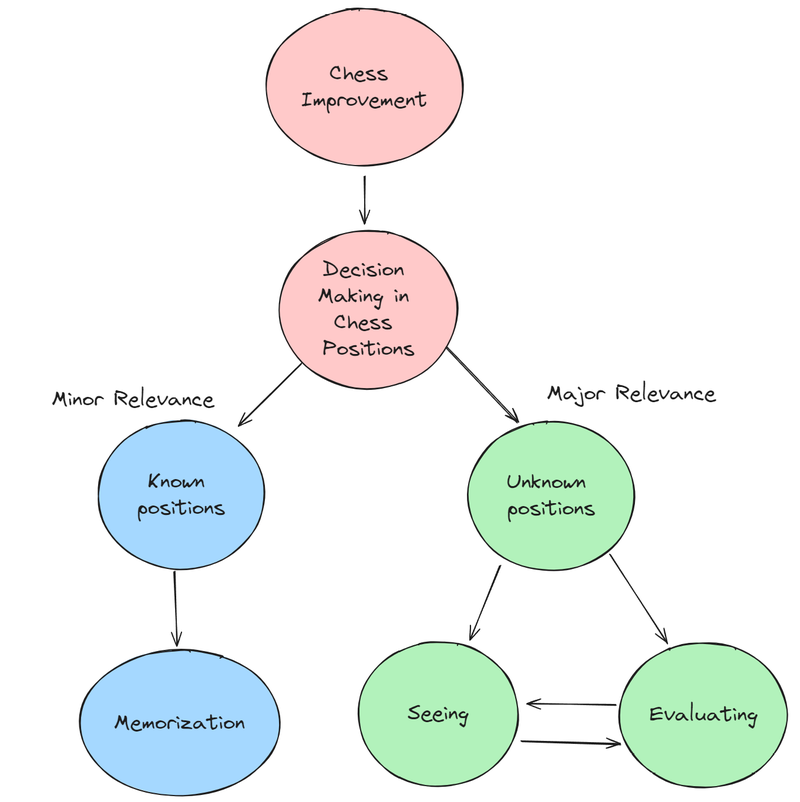
The arrows between seeing and evaluating hints at the interplay between them, which we will discuss in a later article.
Earlier I said that to answer the question of improving at chess, we first must begin with understanding how decisions are made at the chess board. By understanding how decisions are made, we can work to deconstruct the decision-making process into its constituent elements. By identifying these elements, we can pinpoint where our decision-making falters
We have made some progress on this front by identifying two key aspects of this process: seeing and evaluating. Accordingly, we have identified that almost all chess mistakes are either due to flawed vision or flawed evaluation, as noted earlier.
Yet, this is just the beginning. We now have to put each element under the microscope to uncover more. Once we understand the nature of each element more fully, we can then start thinking about how we can improve each process.
In the next article, we will look further at evaluation, and consider the typical perspectives of modern chess culture on this concept. In doing so, we will argue against potentially the most insidious ideal in all of chess – that of justification.
Part 4 of this series is now available here.
